CONDUCTION DE L’ÉLECTRICITÉ

CONDUCTION DE L’ÉLECTRICITÉ

Le terme de conduction électrique désigne l’ensemble des phénomènes qui ont pour effet la transmission d’électricité. L’aptitude d’une substance à conduire l’électricité se mesure par la résistivité ou par son inverse, la conductivité.

L’expérience, dans les cas simples, a mené à la loi d’Ohm: la tension aux bornes d’un échantillon est proportionnelle au courant qui le traverse. Le coefficient de proportionnalité s’appelle résistance et il est fonction de la résistivité de la substance ainsi que de la forme géométrique de l’échantillon.

De façon plus générale, le passage du courant électrique dans la matière sous ses trois états est dû au déplacement de particules chargées. La résistivité est liée, d’une part, au nombre de ces porteurs de charge et, d’autre part, à l’aisance avec laquelle ils peuvent répondre aux sollicitations d’un champ électrique. Les porteurs peuvent être des électrons, comme dans les métaux solides ou liquides, et des ions positifs ou négatifs, comme dans les électrolytes ou dans les gaz. La mobilité est liée aux interactions d’origine coulombienne entre électrons et ions d’une part, entre électrons et électrons d’autre part.

1. Conduction dans les solides

Théorie classique

Elle concerna primitivement les métaux seuls. Néanmoins, une conception unitaire de la conductibilité dans les solides peut être établie.

Depuis le début du siècle, la théorie de la conduction électrique a toujours reposé sur l’idée que le courant électrique était transporté par des particules chargées. Les théories successives ont peu à peu dégagé le nombre des électrons responsables de la conduction et la nature des entraves apportées à leurs déplacements par le réseau ionique et les impuretés.

Vers 1900, Paul Karl Ludwig Drude imagine qu’un métal se compose d’ions lourds, quasi immobiles, et d’électrons qui se déplacent au hasard en se heurtant aux ions. Si un champ électrique 劉 est imposé de l’extérieur, les électrons sont accélérés entre deux collisions dans la direction opposée au champ (loi de Coulomb) et la vitesse moyenne 益 de l’ensemble des électrons cesse d’être nulle pour valoir e 精 劉 / m (e et m sont respectivement la charge algébrique et la masse de l’électron, 2 精 est le temps moyen entre deux collisions). La densité de courant s’obtient en multipliant cette vitesse moyenne par le nombre n d’électrons par unité de volume et par la charge e de l’électron; elle est donc proportionnelle au champ électrique et on retrouve la loi d’Ohm avec pour conductivité électrique: 靖 = n e ² 精 / m .

La théorie de Drude permet également de retrouver la loi empirique de Wiedemann-Franz (1853) selon laquelle, si K est la conductivité thermique, le rapport K/ 靖 à température donnée est le même pour tous les métaux. Pour cela, on considère que l’énergie E et la vitesse moyenne 益 d’un électron dépendent de la répartition de température dans l’échantillon. On montre alors que le flux d’énergie transporté par les électrons est proportionnel au gradient de la température et que la constante de proportionnalité K vaut (2/3)n 精 益²d E/d T, T désignant la température absolue.

Dans ces conditions,

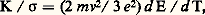et ce rapport est indépendant du métal, pourvu que 益 et E n’en dépendent pas non plus. Ainsi, lorsqu’on applique à l’ensemble des électrons libres du métal, assimilé à un gaz, le résultat de la théorie classique des gaz E = m 益²/2 = 3 k T/2, où k est la constante de Boltzmann, on trouve:

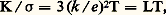où L est le nombre de Lorenz (cet auteur avait montré dès 1872 que K/ 靖 était proportionnel à T).

La valeur calculée pour L à partir de k et de e (0,2232 行) était en accord satisfaisant avec les valeurs expérimentales trouvées à température ambiante:

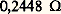Toutefois, prises séparément, les formules de K et de 靖 ne sont pas sans soulever certaines difficultés, notamment dans la façon inexplicable dont n varie avec la température.

Ludwig V. Lorenz a précisé cette théorie sur deux points: d’une part, il a employé la notion de fonction de distribution des électrons et, d’autre part, il a mieux défini les mécanismes de collision. Par définition, la fonction de distribution f (k 轢, r 轢, t ) est telle que f (k 轢, r 轢, t ) drdkreprésente le nombre moyen d’électrons situés à l’instant t dans l’élément de volume drautour du point repéré par r 轢, et tels que les extrémités des vecteurs représentant leurs moments cinétiques se trouvent dans le volume dkde l’espace réciproque (espace des moments cinétiques) situé autour de k 轢. La conservation des électrons dans l’espace à six dimensions (k憐 r 轢) conduit à l’équation de Boltzmann:

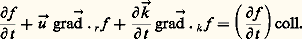dans laquelle, uest la vitesse des électrons. Le second membre de cette équation traduit l’effet des collisions subies par ces électrons. Lorenz supposa que les électrons rebondissent de façon élastique sur les ions considérés comme des sphères fixes. Il utilisa la fonction f ⁰ de la statistique de Maxwell-Boltzmann et détermina ainsi f , puis le courant électrique, K et 靖. Cependant, après cette refonte, demeurent des objections de même nature que celles que soulève la présentation de Drude.

Théorie quantique

Il faut attendre 1928 pour qu’un progrès sensible soit réalisé par Arnold Sommerfeld qui conjugue l’usage de la distribution de Fermi-Dirac et la mécanique quantique sans toutefois préciser la nature périodique de l’interaction entre les ions et les électrons. On trouvait ainsi:

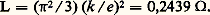et l’accord avec l’expérience était excellent. Cependant les valeurs à donner au libre parcours moyen pour trouver les valeurs exactes de 靖 demeuraient inexpliquées.

L’étape suivante consista à tenir compte de l’interaction périodique dans l’espace qui existe entre l’électron et le réseau cristallin. Félix Bloch (1928) montra qu’un électron se déplace sans résistance dans un réseau parfait immobile . Le libre parcours moyen ne correspond donc pas aux chocs des électrons sur les ions proprement dits mais à l’interaction plus espacée de l’électron avec, d’une part, les impuretés ou imperfections du réseau cristallin (terme indépendant de la température) et avec, d’autre part, une particule fictive, le phonon, représentant les mouvements d’oscillation thermique des ions du réseau (terme croissant lorsque la température croît et prédominant aux températures ambiantes). On retrouva ainsi la loi expérimentale d’Auguste Matthiessen; bien plus, on put définir clairement quels étaient ceux des électrons libres qui prenaient part à la conduction.

Dans un réseau ionique de symétries déterminées, on établit l’existence des zones de Brillouin ou portions de l’espace réciproque (espace k 轢) que peut «occuper» un électron. Il est possible de calculer l’énergie que prend cet électron en chaque point de cette zone. Dans une même zone, l’ensemble des énergies est continu et constitue la bande d’énergie. Les intervalles d’énergie de deux zones différentes peuvent se recouvrir ou être séparés par une bande interdite (gap ). L’ensemble des états occupés s’obtient en multipliant l’ensemble des états disponibles par la fonction de Fermi-Dirac f (E) qui ne dépend que de l’énergie E de l’état considéré:

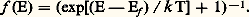Dans cette expression apparaît E^f , énergie de Fermi caractéristique du corps, telle que le produit de f (E) par la densité des états disponibles, intégré sur toutes les énergies, donne le nombre total d’électrons (libres et liés) par unité de volume. Selon la position de E^f par rapport aux limites des bandes, ces dernières seront complètes, partiellement remplies ou vides (fig. 2).

Dans une bande complètement remplie, les électrons ont deux à deux des vitesses opposées et aucun courant ne peut passer tant que le champ électrique n’a pas atteint une valeur telle que des électrons soient enlevés à la dernière bande remplie et portés dans la première bande vide: le corps est dit isolant. Au contraire, si la bande est incomplètement remplie, un faible champ électrique suffit à changer la répartition des électrons de manière à ce qu’une direction de déplacement prédomine; le corps est dit métallique.

Quand enfin la température est telle que coexistent une bande presque pleine et une autre presque vide, ce qui suppose un «gap» de l’ordre de quelques k T, les nombreux électrons de la bande remplie (bande de valence) disposeront de quelques places tandis que les quelques électrons de la bande peu peuplée (bande de conduction) auront plus de chances d’obéir au champ électrique et de se déplacer à l’unisson. La conductivité sera moyenne et le corps est dit semi-conducteur. Dans le calcul de la conductivité, on devra tenir compte des électrons de la bande de conduction et ajouter leurs contributions à celles des électrons de valence. Pour rendre le calcul plus aisé on préfère suivre le déplacement des «trous» (places vides de la bande de valence assimilées à des particules chargées) et ajouter leurs effets à ceux des électrons de conduction.

Propriétés des métaux

La conductivité des métaux et leurs propriétés mécaniques leur font jouer un grand rôle industriel dans le domaine de l’électricité. Le cuivre et l’aluminium sont choisis pour transporter le courant électrique en raison de leur très basse résistivité aux températures ordinaires. Au contraire, pour le chauffage et l’éclairage, on choisira un métal fortement résistant de façon à dissiper le plus possible d’énergie sous réserve que ses autres propriétés physiques lui permettent de supporter de tels échauffements. Il en est ainsi du tungstène pour l’éclairage par incandescence. Le tableau donne les résistivités d’un grand nombre de métaux, exprimées en unités pratiques. L’unité de résistance dans le système international est l’ohm.

La loi de Matthiessen exprime la résistivité par: 福 = 福^r + 福(T). Aux températures usuelles, le terme 福^r dû aux impuretés est généralement faible devant le terme dépendant de la température 福(T) et on se contente d’écrire 福 = 福⁰ (1 + 見t ), où 福⁰ est la résistivité à 0 ⁰C, 見 un coefficient propre au métal mais toujours de l’ordre de 4 . 10^-3 si t , la température, est exprimée en degrés Celsius. Pour des températures plus élevées (au-delà de 100 ⁰C environ), 福 croît plus rapidement sauf pour le platine et le palladium.

Aux très basses températures, c’est-à-dire dans l’hélium liquide (vers 4 K), la distinction entre 福^r et 福(T) apparaît d’autant mieux que 福(T) varie comme une puissance élevée de la température absolue T. Cette puissance est de 5 pour l’or, ce qui, selon la théorie, correspond au cas où le métal peut être assimilé à un gaz d’électrons libres. 福(T) varie en ² ou ³ quand existe une interaction électron-électron, ce qui semble être le cas pour de nombreux métaux de transition.

D’après ce qui a été dit, on peut démontrer que la résistivité d’un semi-conducteur décroît exponentiellement avec la température.

Les métaux ferromagnétiques (nickel, fer, cobalt et alliages) ont une résistivité qui croît anormalement aux alentours de leur point de Curie. À très basse température, une faible concentration d’impuretés ferromagnétiques de ce type dans un métal ordinaire entraîne l’apparition d’un minimum de la résistivité (dans La⁰,⁹⁴Ce⁰,⁰⁶; T minimum = 8 K). Cet effet Kondo s’interprète en termes d’interaction entre les spins des électrons de conduction et celui de l’impureté fixée dans le métal.

En général, la résistivité d’un alliage dépend de la façon dont il est constitué. Si les deux métaux précipitent séparément, la conductivité est une moyenne pondérée des conductivités des métaux purs. S’il y a insertion ou substitution, la résistivité résiduelle 福^r de la solution solide ainsi constituée est plus forte que la moyenne pondérée des résistivités de chacun des métaux purs, et cela d’autant plus que les deux espèces d’atomes diffèrent davantage.

La résistivité décroît généralement lorsque la pression croît. Pour le cuivre, le rapport de la résistivité sous 100 000 kg/cm² à la résistivité sous pression nulle est de 0,866. Font exception à cette règle les corps suivants: baryum (2,618), calcium (4,399), césium (5,33), lithium (1,704), rubidium (2,95) et strontium (1,810).

Un champ magnétique diminue la résistivité des métaux ferromagnétiques et augmente celle des autres métaux. Cet effet est d’autant plus sensible que la température est plus basse et que le champ magnétique est perpendiculaire au courant. Le bismuth se signale par l’importance de ses variations de résistivité, si bien qu’il sert à la mesure des champs magnétiques. Ce phénomène de magnétorésistance ne doit pas être confondu avec l’effet Hall.

L’expérience montre que la résistance d’un conducteur, soumis à un champ électrique alternatif de haute fréquence, varie avec la valeur de cette fréquence. Ce phénomène est appelé effet de peau. La théorie montre qu’il y a concentration des lignes de courant vers la surface extérieure du conducteur. Le courant décroît exponentiellement à partir de la surface et la profondeur de peau caractéristique est donnée par: 嗀 = 連 福/ 神猪f , où 猪 est la perméabilité du métal et f la fréquence. Pour du cuivre, à 100 MHz, 嗀 est de l’ordre de 6,5 . 10^-6 m.

Si la profondeur de peau devient plus faible que la distance moyenne entre deux collisions, ce qui arrive à haute fréquence pour des températures suffisamment basses, les électrons échappent à l’action du champ électrique pendant une partie de leur parcours entre deux chocs. La résistance est alors plus forte que prévue. Cet effet est appelé effet de peau anormal.

Les propriétés détaillées des semi-conducteurs, des isolants et des supra-conducteurs ne sont pas abordées ici, non plus que les phénomènes de conduction ionique et de photoconductivité dans les solides.

2. Conduction dans les liquides

Conduction dans les électrolytes

Définitions

La dissolution d’un corps, appelé électrolyte, dans un autre corps appelé solvant (tel que l’eau) s’accompagne d’une dissociation des molécules donnant naissance à des ions chargés électriquement, les cations (charge positive) et les anions (charge négative). Dans la suite, les grandeurs physiques relatives aux cations et aux anions seront respectivement affectées des indices c et a .

À cette dissociation peuvent se superposer des réactions d’interaction entre les ions issus du soluté et ceux du solvant; il y a alors naissance d’ions complexes nouveaux à côté des ions élémentaires ou des molécules appartenant, soit au soluté, soit au solvant.

Lorsque l’on applique une différence de potentiel à un tel liquide, on crée en son sein un champ électrique dans lequel les ions chargés se déplacent.

Le nombre de molécules dissociées divisé par le nombre total de molécules est le degré de dissociation 見. Il croît avec la dilution et vaut l’unité pour une dilution infinie. On distingue les électrolytes forts à peu près complètement dissociés à toutes concentrations (acides et bases fortes et la plupart des sels) et les électrolytes faibles dont le degré de dissociation dépend de la concentration (eau, acides et bases organiques, quelques acides minéraux).

Si l’électrolyte comprend une seule espèce d’ion positif et une seule espèce d’ion négatif, la conductivité électrique est donnée par: 靖 = C 見N |e | ( 猪^c + 猪^a ), où N est le nombre d’Avogadro, e la charge de l’électron, C la concentration en équivalent-gramme, 猪^c et 猪^a les mobilités des cations et des anions.

On appelle équivalent-gramme la quantité de matière correspondant à un ion-gramme divisée par la valence; par exemple, la concentration en équivalent-gramme d’un ion-gramme de calcium en solution est 40/2. Les mobilités sont définies par les deux relations:

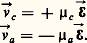L’unité usuelle de conductivité est 行^-1 . cm^-1, on désigne parfois l’inverse de l’ohm par mho ou siemens (S). Souvent on utilise la notion de conductivité équivalente: 炙 = 靖/C. Si la dilution est infinie ( 見 = 1) la conductivité équivalente vaut 炙⁰ = N |e | ( 猪^c + 猪^a ).

Problèmes théoriques

En 1884, Arrhénius proposa une théorie de la dissociation électrolytique. Il émit l’hypothèse que la décroissance de 炙 lorsque C croît est due à la décroissance du nombre d’ions conducteurs, leur mobilité étant inchangée, ce qui amène à poser 見 = 炙/ 炙⁰. Ce modèle n’est valable que pour les électrolytes faibles qui suivent la loi de dilution d’Ostwald et l’on a:

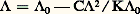où K est la constante d’équilibre ionique. Une équation de ce type est assez satisfaisante pour les électrolytes faibles peu concentrés si l’on tient compte du comportement non idéal des ions et de la décroissance de la mobilité ionique avec la concentration.

La difficulté théorique repose sur le calcul des interactions entre les ions. En 1923, Peter J. W. Debye et Erich Hückel présentèrent un calcul de ces interactions et Lars Onsager l’appliqua au calcul de la conductivité en 1927. Les interactions entre ions sont conditionnées, d’une part, par les forces électrostatiques qui ont tendance à donner aux ions un arrangement défini et, d’autre part, par le mouvement thermique qui tend à produire une répartition aléatoire. En solution, autour d’un ion de polarité définie et en moyenne dans le temps, il y aura plus d’ions de polarité opposée que si la répartition était aléatoire.

Deux effets ont tendance à réduire la mobilité ionique lorsque la concentration augmente:

– L’environnement d’un ion donné est constitué d’ions de charge opposée auxquels sont associées des molécules neutres de solvant. Sous l’action d’un champ électrique, cet environnement tend à se déplacer dans la direction opposée à celle de l’ion considéré et ralentit donc son mouvement. Cet effet, analogue à une augmentation de la viscosité du milieu, est appelé effet électrophorétique.

– Sans champ extérieur, l’environnement d’un ion donné est de symétrie sphérique et le centre de gravité des charges électriques est sur cet ion central. Si la solution est soumise à un champ électrique, l’ion central se déplace en entraînant avec lui son entourage dont le déplacement, bien que rapide, n’est pas instantané (temps de relaxation). Il y a donc distorsion de l’atmosphère entourant l’ion central et le centre de gravité des charges électriques est alors décalé derrière cet ion, créant ainsi une force électrostatique qui le freine dans son mouvement dans la direction du champ. C’est l’effet du temps de relaxation.

L’équation établie par Onsager, tenant compte de ces effets pour les solutions électrolytiques très diluées est:

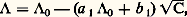ou a ¹ et b ¹ sont des constantes dépendant de la nature du solvant et de la température. Cette relation est correcte pour les électrolytes forts très dilués, cependant la conductivité équivalente expérimentale est plus grande que la conductivité équivalente donnée par l’équation ci-dessus, lorsque la concentration augmente. En considérant la taille des ions, Raymond M. Fuoss et Lars Onsager ont trouvé en 1957 une expression plus précise:

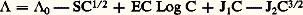où J¹ et J² sont des constantes tenant compte de la distance minimale d’approche des ions libres et des propriétés du solvant. Fuoss et Onsager ont publié ensuite une théorie révisée de la conductivité des électrolytes symétriques. L’équation obtenue présente de nombreuses analogies avec l’équation donnée plus haut, elle comprend des termes complémentaires qui doivent améliorer l’accord entre l’expérience et la théorie pour les électrolytes forts à concentration moyenne.

En conclusion, on peut dire qu’actuellement l’accord entre les théories et les résultats expérimentaux est assez bon pour les électrolytes faibles et forts en solutions relativement diluées (jusqu’à 0,1 N environ). Il n’y a pas de théorie satisfaisante pour les électrolytes concentrés et pour les sels fondus. Cela est dû en partie à l’ignorance où l’on est des détails du comportement du solvant au niveau moléculaire, spécialement dans le cas de l’eau, et également à l’ignorance de l’interaction coulombienne entre ions à forte concentration.

Conductivité des métaux liquides

Expérimentalement, la résistivité électrique d’un métal à l’état liquide peut, en général, se mettre sous la forme:

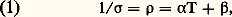où T est la température absolue. N. E. Cusack, en 1963, a réuni l’ensemble des propriétés électroniques des métaux liquides. Pour les métaux alcalins liquides, la résistivité est relativement faible (Na: 9,6 猪行 . cm); elle est en général plus élevée pour les autres métaux, en particulier pour les métaux de transition (Fe, Co, Ni) et les semi-métaux (Sb, Bi) dont la résistivité est de l’ordre de 100 猪行 . cm. Le mercure (91 猪行 . cm) fait exception; on verra qu’il pose un problème particulier. Le coefficient de température 見 est de l’ordre de 10^-2 à 10^-1/K. La résistivité de quelques métaux (Zn, Cd, Hg) ne suit pas l’équation (1).

Dans les métaux liquides, les conductivités électrique et thermique sont dues aux électrons et suivent, comme dans les métaux solides, la loi de Wiedemann-Franz.

Les mesures de l’effet Hall relatives aux métaux liquides ont montré que l’on pouvait appliquer le modèle des électrons presque libres (N.F.E. dans la littérature anglo-saxone). Le nombre d’électrons participant à la conduction est alors égal à celui des électrons de valence. Connaissant la densité du liquide, on calcule de façon très simple le nombre de porteurs de charge par unité de volume n entrant dans la relation 靖 = ne 猪. Les mesures de 靖 ont permis de déduire la mobilité 猪 des électrons; elle varie de 0,5 cm²/V. s pour les semi-métaux à 10 pour les alcalins.

En 1961, Ziman a développé une théorie des métaux liquides monovalents. En 1962 et en 1965 avec Bradley, Faber et Wilson, il a étendu cette théorie aux métaux polyvalents et aux alliages binaires. Tenant compte, d’une part, de la position des atomes au sein du liquide et, d’autre part, de l’interaction entre les électrons et les ions, il obtint la formule: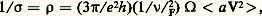

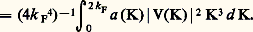où: face=F0019 麗a V² 礪

行 est le volume occupé par un atome, k ^F et 益^F sont le vecteur d’onde et la vitesse au niveau de Fermi. a (K) (fonction de corrélation) est la transformée de Fourier de la fonction de distribution radiale (R.D.F.) caractérisant la régularité de la disposition des atomes entourant un atome donné. Cette fonction de distribution radiale est calculée à partir des intensités diffractées par le liquide soumis à un faisceau de rayons X ou de neutrons. V(K) est la transformée de Fourier du pseudo-potentiel relatif au liquide considéré. Ce pseudo-potentiel doit tenir compte de l’interaction effective totale électron-ion (incluant l’effet d’écran) dans les collisions des électrons de Fermi. Ce dernier problème est difficile; des modèles théoriques de pseudo-potentiel ont été proposés (W. A. Harrison, 1966).

L’accord entre l’expérience et la théorie précédente est relativement bon lorsque les fonctions a (K) et V(K) sont connues avec une précision suffisante dans toute la région d’intégration 0-2 k ^F (J. L. Sundström, 1964; Ashcroft, 1966).

Un problème particulier se pose pour le mercure dont la résistivité est anormalement haute et que les impuretés font rapidement baisser cette résistivité. N. F. Mott, en 1966, a suggéré que, dans ce cas, la densité d’états au niveau de Fermi peut être plus faible que la densité obtenue dans le modèle des électrons libres.

Signalons encore qu’il existe un certain nombre de liquides simples (Se, Te) ou plus complexes (certains séléniures, tellurures et oxydes) dont les propriétés sont plus proches de celles des semi-conducteurs solides que de celles des métaux liquides. La théorie de la conduction électrique dans de tels liquides n’est pas encore élaborée.

3. Conduction dans les gaz

Ionisation des gaz. Collisions

Dans les conditions normales, les gaz sont composés d’atomes neutres et de molécules, ils ne sont donc pas des conducteurs de l’électricité. Cependant, lorsqu’ils sont soumis à des influences extérieures permettant leur ionisation, ils peuvent conduire le courant. Pour obtenir cette ionisation, il est nécessaire d’arracher les électrons des couches externes des atomes constituant le gaz, ce qui nécessite la mise en jeu d’une énergie de l’ordre de 5 à 25 eV. Si l’on fournit des énergies plus faibles, il y aura excitation des atomes avec changements d’orbite des électrons, ceux-ci revenant à leur état initial avec émission de rayonnement; cela est à l’origine des phénomènes lumineux observés dans les gaz ionisés. L’énergie nécessaire à l’ionisation peut être fournie par agitation thermique (gaz portés à haute température: plasmas) ou par application d’un champ électrique suffisamment intense. On se limitera ici aux phénomènes de base dominant la conduction de l’électricité dans le gaz. On laissera de côté les phénomènes prédisruptifs et disruptifs qui diffèrent suivant les gaz, la répartition des champs électriques appliqués et la pression. On ne parlera pas non plus de la conduction dans les plasmas.

Un gaz quelconque contient presque invariablement quelques ions et électrons donnant une conductivité extrêmement faible.

Il existe une ionisation résiduelle provenant des rayons cosmiques, de la radio-activité naturelle du globe terrestre ou de la lumière par effet photo-électrique sur les métaux en contact avec le gaz. Cette ionisation joue un grand rôle, créant une source initiale d’électrons nécessaires au «claquage» d’un gaz. Les atomes d’un gaz se heurtent entre eux et avec les électrons et les ions. Le libre parcours moyen d’un atome entre deux chocs est d’environ 10^-4 cm pour l’air ambiant. On a la relation: l = 1/P^c p , où l est le libre parcours moyen (exprimé ici en cm), p la pression (en mm de Hg) et P^c une constante de proportionnalité qui dépend du gaz et de la vitesse des particules entrant en collision. Dans les gaz usuels, P^c est de l’ordre de 5 à 100 (cm . mm-Hg)^-1 pour les collisions entre électrons et atomes; cette valeur peut être dix fois plus grande pour les vapeurs métalliques.

À toute température absolue, T, les atomes gazeux, les électrons et les ions sont en mouvement. La théorie cinétique des gaz montre que l’énergie cinétique moyenne d’une particule de vitesse moyenne v et de masse m est mv ² = (3/2) k T. Comme la température d’un mélange de particules en équilibre est uniforme, nous voyons que la vitesse v est plus grande pour les particules légères. Par exemple, les atomes de l’air à température ambiante ont une vitesse de l’ordre de 4 . 10⁴ cm/s, alors que celle des électrons est de l’ordre de 10⁷ cm/s. Ceci est vrai en moyenne; en réalité, il y a, pour un type de particules, une distribution maxwellienne des vitesses proportionnelle à:

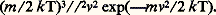Gaz soumis à un champ électrique

Si l’on applique au gaz un champ électrique 轢 劉, la force agissant sur la particule de charge q , entre deux chocs de celle-ci, est q 轢 劉. Ainsi, la vitesse moyenne, donc l’énergie de cette particule chargée, augmente. Un nouvel équilibre s’établit où les particules chargées, d’une part, gagnent de l’énergie grâce au champ électrique appliqué et, d’autre part, en restituent aux atomes étrangers lors des collisions. L’énergie d’équilibre est déterminée par la quantité d’énergie fournie par le champ électrique entre deux chocs, soit 劉l . Or, comme le libre parcours moyen l est inversement proportionnel à la pression, on peut dire que l’énergie moyenne de la particule est une fonction de 劉/p , fonction dépendant de la charge et du gaz étudié. Dans un champ électrique, les particules chargées acquièrent une vitesse d’entraînement v ^D = |q | l 劉/mv , où v est la vitesse d’agitation thermique dépendant de 劉/p ; comme 劉l est fonction de 劉/p , 益^D en dépend aussi. On définit ici la mobilité 猪 par v ^D = 猪 劉 avec 猪 = |q | l /mv .

S’il y a n particules chargées par unité de volume, la densité de courant est J = n |q |v ^D, ce qui permet alors de définir la conductivité par 靖 = J/ 劉 = n |q | 猪.

En fait, dans un gaz ionisé où il y a généralement des ions positifs et des électrons, on peut écrire, en supposant les particules indépendantes:

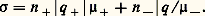Dans la plupart des cas, v ^D est proportionnelle à 劉/p donc, à pression constante, proportionnelle à 劉. Ainsi 靖 est presque indépendante du champ électrique et le courant dans le gaz suit la loi d’Ohm. Mais cela n’est pas généralisable.

La mobilité des ions est beaucoup plus faible que celle des électrons. S’il y a un nombre à peu près égal d’électrons et d’ions, presque tout le courant résultera des électrons.

Dans un certain nombre de gaz, les atomes sont incapables de fixer des électrons, on caractérise alors le gaz par son coefficient d’ionisation 見 qui est par définition égal au nombre de chocs ionisants qu’un électron peut produire par cm de parcours dans la direction du champ.

Ce coefficient 見, appelé premier coefficient de Townsend, est lui aussi une fonction de 劉/p , en général du type:

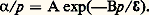Le nombre n d’électrons, abordant un trajet x dans la direction du champ, sera multiplié à l’issue de ce parcours par le coefficient de multiplication:

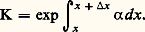Dans beaucoup de gaz, les électrons libres ont tendance à s’attacher aux atomes neutres en formant des ions négatifs assez stables. Cet effet d’attachement est très prononcé dans certains gaz (oxygène, halogènes, S⁶). La mobilité des ions négatifs est faible et de l’ordre de celle des ions positifs; ces gaz auront donc une très faible conductivité et leur claquage sera difficile; ils seront utilisés comme isolants. Pour ces gaz, il est nécessaire de définir un coefficient d’attachement 兀 représentant la probabilité de capture d’un électron lorsque celui-ci fait un parcours de 1 cm dans la direction du champ. En général 兀 dépend de 劉/p de la même manière que 見. Le coefficient de multiplication dans un tel gaz est alors:

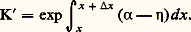Signalons que, dans certains cas, les ions positifs peuvent, en frappant une surface métallique, créer une émission d’électrons secondaires. L’ion est alors neutralisé par un électron du métal et il existe une probabilité 塚ⁱ pour qu’un second électron soit émis. Comme une énergie égale au travail d’extraction est requise pour arracher chaque électron, le phénomène n’est possible que si le potentiel d’ionisation excède deux fois le travail d’extraction.

Encyclopédie Universelle. 2012.